Infinity: The Story So Far
(Revised: 2018-04-11)

� Javier Regueira-Serrano

Introduction

What is an infinte set? To answer this question, we will first develop a non-numeric notion of a finite set. Then an infinite set will simply be one that is not finite. We begin by going for a leisurely walk through this ancient village.

A Walk Through a Finite Village

Starting at any house in this finite village, you set out to visit some or all of the houses there. You keep walking non-stop until you return to your starting point, visiting no house more than once.

Intuitively, it seems obvious that you could not avoid returning to your starting point under these conditions. You could, of course, return to your starting point without first going to every other house in the village. If you kept going, however, you would eventually run out of different places to go, and you would have to return to your starting point. Going anywhere else at that point would be going there more than once. (As you might imagine, in an infinite village, it might be possible to keep walking from house to house, never stopping and never returning to your starting point.)

How can we describe such paths mathematically? We can begin by letting S be the set of houses in the village. Each path that you can take through the village can be specified by:

1. Your starting pointing at house x₀

2. A relation f on S that specifies the order in which you will visit the houses in S.

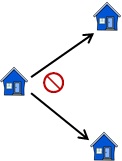
For every house in S on your path, you will go next to exactly one house in S. Therefore,  f is a function on S.

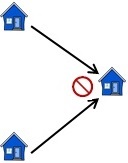
Figure 1:  Relation f is a function on S.

You cannot go to the same house more than once, i.e. function f is injective.

Figure 2:  Function f is injective.

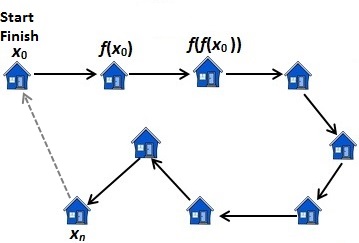
Figure 3:  Example of a walk starting and finishing at house x₀. House x_n
is the last house visited before returning to house x₀.

How do we specify that you must return to your starting point x₀? Simply by requiring that there must exist a house x_n in the village such that f(x_n) = x₀. (See figure 3, dashed line.)

Thus, we can define set S to be finite if and only if for all x₀ and f, if x₀ e S and f is an injective  function mapping S to itself, then there must exist x_n e S such that f(x_n) = x₀.

In DC Proof format:

ALL(s):[Set(s) => [FiniteA(s)
<=> ALL(x0):ALL(f):[x0 e s
& ALL(a):[a e s => f(a) e s]
& ALL(a):ALL(b):[a e s & b e s => [f(a)=f(b) => a=b]]
=> EXIST(xn):[xn e s & f(xn)=x0]]]]

An Equivalent Definition of Finite (Dedekind)

First introduced by Richard Dedekind, here is an equivalent and somewhat easier definition to work with:

ALL(s):[Set(s) => [Finite(s)
<=> ALL(f):[ALL(a):[a e s => f(a) e s]
& ALL(a):ALL(b):[a e s & b e s => [f(a)=f(b) => a=b]]
=> ALL(a):[a e s => EXIST(xn):[xn e s & f(xn)=a]]]   Formal Proof (55 lines)

In words, a set S is finite if and only if for all functions f mapping S to itself, if f is injective (1-to-1) , then f is surjective (onto).

The Infinite as the Negation of the Finite

In walking through an infinite village, there would be no guarantee, as above, that you would ever return to your starting point. Not surprisingly then, a set is infinite if and only it is not finite. Thus, we define Infinite as follows:

ALL(s):[Set(s) => [Infinite(s)
<=> EXIST(f):[ALL(a):[a e s => f(a) e s]
& [Injection(f,s,s)
& ~Surjection(f,s,s)]]]]

where

Infinte(x) means x is infinite
Injection(f,x,y) means f is an injection (1-to-1) mapping set x to set y
Surjection(f,x,y) means f is an surjection (onto) mapping set x to set y

In words, a set S is infinite if and only if there exists a function f mapping S to itself that is injective (1-to-1) and not surjective (not onto).

An Equivalent, Numerically-based Definition of Infinite

Suppose we are given the set N, 0 e N and a successor function next that satisfy the Peano axioms. Then we can then develop the following equivalent definition of infinite:

ALL(s):[Set(s) => [Infinite(s)
<=> EXIST(f):[ALL(a):[a e n => f(a) e s]
& ALL(a):ALL(b):[a e n & b e n => [f(a)=f(b) => a=b]]]]]  Formal Proof (515 lines)

Or equivalently:

ALL(s):[Set(s) => [Infinite(s)
<=> EXIST(f):[ALL(a):[a e n => f(a) e s]
& Injection(f,n,s)]]]

In words, a set S is infinite if and only if there exists an injective function (1-to-1) mapping N into S.

Countable Sets

A set S is said to countable if and only there exists an injective function mapping S into N. (Note similarities to previous definition.)

ALL(s):[Countable(s)
<=> EXIST(f):[ALL(b):[b e s => f(b) e n]
& Injection(f,s,n)]]

A countable set S may be finite or infinite. If S is countable and infinite, there exists a bijection mapping S to N (see Cantor-Bernstein-Schroeder Theorem).

It is trivial to show that the set of natural numbers N must itself be countable.

Cantor's Theorem

Let P be the power set of S. (S may be finite or infinite.) Then there exists no surjective function mapping S onto P.

ALL(s):ALL(p):[Set(s)
& Set(p)
& ALL(c):[c e p <=> Set(c) & ALL(d):[d e c => d e s]]
=> ALL(f):[ALL(a):[a e s => f(a) e p] => ~Surjection(f,s,p]]]  Formal Proof (53 lines)

Thus, we can never cover the entire power set P with images of S under any function mapping S to P. This suggests that the power set of a set S is always somehow larger than S itself, even if S is infinite. This, in turn, suggests that some infinities are larger than others.

It is easy to prove that the set of natural numbers N and its power set are both, by definition, infinite. Cantor's Theorem suggests that the power set of N, in particular is somehow larger than N itself.

The power set of N is uncountable

Let PN be the power set of the set of natural numbers N:

ALL(a):[a e pn <=> Set(a) & ALL(b):[b e a => b e n]]

Then PN is not countable:

~Countable(pn) Formal Proof (25 lines)

Home